If you’ve ever taken a course on linear regression, you probably learned that ordinary least squares (OLS) is BLUE—the best linear unbiased estimator. Great mnemonic, great property! Who doesn’t want the best?
Best, in this context, means minimum sampling variance, something that’s definitely desirable. But it’s more than a little annoying that OLS is only “best in class”—the class of linear unbiased estimators. That leaves open the possibility that a non-linear or biased estimator could have even smaller sampling variance. Indeed, maximum likelihood estimation of a regression model with non-normal errors (e.g., an extreme-value distribution) will typically be both biased and non-linear. In those cases, maximum likelihood will usually have smaller sampling variance than OLS.
When I teach linear regression, I find that students have no difficulty understanding that OLS is unbiased. But I often struggle to explain what it means for a regression estimator to be linear (more on that shortly). So, I was delighted to learn that economist Bruce Hansen (2022) had proved that the linearity restriction was not necessary. According to Hansen, OLS has the lowest sampling variance among all unbiased estimators, both linear and non-linear. In other words, OLS is BUE—the best unbiased estimator.
LEARN MORE IN A SEMINAR WITH PAUL ALLISON
This is a big deal. The proof that OLS is BLUE, known as the Gauss-Markov theorem, had its initial formulation by Gauss more than 200 years ago. Since then, the assumptions about the error term in the regression model have been relaxed in several ways. For example, Gauss assumed normality, but Markov (80 years later) showed that there was no need for normality—homoscedasticity and zero autocorrelation are sufficient. But no one ever suggested that the linearity condition could be dropped.
Hansen’s proof is long and difficult (at least for me), but the fact that it was published in Econometrica gave me some assurance that it’s correct. Unfortunately, that assurance was short-lived. Before Hansen’s paper even made it into print, Pötscher and Preinerstorfer (2022) vigorously attacked his results, stating that
[Hansen makes] several assertions from which he claims it would follow that the linearity condition can be dropped from the Gauss-Markov Theorem or from the Aitken Theorem [a generalization of Gauss-Markov]. We show that this conclusion is unwarranted, as his assertions on which this conclusion rests turn out to be only (intransparent) reformulations of the classical Gauss-Markov or the classical Aitken Theorem, into which he has reintroduced linearity through the backdoor, or contain extra assumptions alien to the Gauss-Markov or Aitken Theorem.
Oh jeez, that doesn’t sound good at all! Backdoor linearity? Intransparent reformulations? Alien assumptions? How embarrassing for Hansen!
P&P’s paper is at least as technical as Hansen’s, so I was left in a quandary about whom to believe. I figured I had better wait until the dust settled before I wrote anything about this statistical kerfuffle.
Well, the dust has settled, to some degree, and I’ll share that news in a moment. But first, a brief digression into what it means for a regression estimator to be linear—exactly what I hate spending time on in my linear regression course. (If you hate it too, feel free to skip down to the paragraph that starts “Now comes the question…”).
The first hurdle to get over is that the linearity of the estimator has nothing to do with the linearity of the regression model. Simply put, a linear estimator of regression parameters is one that can be expressed as a linear combination of the values of the dependent variable.
For a bivariate regression of y on x, a linear estimator of the slope coefficient is one that can be written as
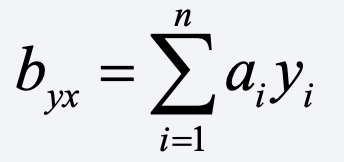
where the a’s are some function of the x’s. In the case of OLS,
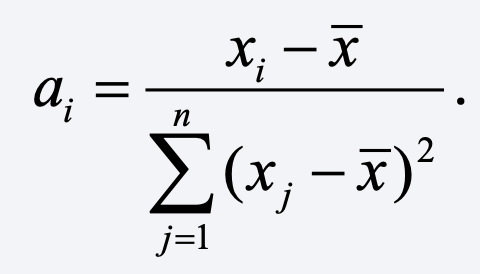
For multiple regression with n observations and k coefficients (including the intercept), a linear estimator of the coefficients can be expressed in matrix notation as
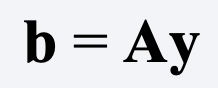
where y is an n x 1 vector of values of the dependent variable and A is some k x n matrix. In the case of OLS,
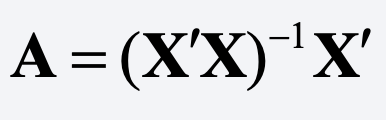
where X is the n x k matrix of values of the predictor variables (including a column of 1s for the intercept).
For some matrix A, what does it mean to claim that Ay is unbiased? Essentially, it means that the expected value of Ay is equal to the vector of true regression coefficients, i.e., E(Ay) = β. Are there any unbiased estimators of the form Ay that are not OLS? Absolutely! We can get one just by deleting m observations at random from the data set. But that would obviously have larger sampling variance than OLS.
More generally, under the classic linear regression model, any weighted least squares (WLS) estimator that assigns unequal weights to the observations will be unbiased. But again, the sampling variance of the WLS estimator will be greater than that of OLS—unless the error variances differ across observations (heteroscedasticity) and the weights are the inverse of those variances.
Now comes the question that is crucial to resolving the disagreement between Hansen and his detractors. Are there any unbiased estimators of β that are not linear? In the latest issue of The American Statistician, Stephen Portnoy (2022) concludes that the answer is no! Based on another highly technical proof, Portnoy states that “for general linear models, any estimator that is unbiased for all distributions in a sufficiently broad family must be linear.”
Portnoy had the advantage of studying both Hansen’s paper and P&P’s critique, and his conclusion seems to be that both papers are, in some sense, correct. Hansen is correct when he says that OLS is the best unbiased estimator. But since unbiasedness implies linearity in this case, it’s really no different than saying it’s the best linear unbiased estimator.
Is this the final word? I hope so. The upshot for me is that we teachers of regression analysis can finally dispense with having to explain what a linear estimator is. OLS is BUE, pure and simple. We can just hold in our hearts the knowledge that the set of non-linear unbiased estimators of the classic linear regression model is empty. Why complicate things?
The only downside? BLUE is a much cooler acronym than BUE. I’ll miss it.
REFERENCES
Hansen, B. E. (2022). A Modern Gauss–Markov Theorem. Econometrica, 90(3), 1283-1294. https://doi.org/10.3982/ECTA19255
Portnoy, S. (2022). Linearity of unbiased linear model estimators. The American Statistician, (just-accepted), 1-10. https://doi.org/10.1080/00031305.2022.2076743
Pötscher, B. M., & Preinerstorfer, D. (2022). A Modern Gauss-Markov Theorem? Really?. arXiv preprint arXiv:2203.01425. https://doi.org/10.48550/arXiv.2203.01425


