In my courses and books on longitudinal data analysis, I spend a lot of time talking about the between-within model for fixed effects. I used to call it the hybrid model, but others have convinced me that “between-within” provides a more meaningful description.
Last week my long-time collaborator, Paula England, asked me a question about the between-within model that stumped me at first. When I finally figured out the answer, I realized that it could potentially be important to anyone who uses the between-within method. Hence, this post.
LEARN MORE IN A SEMINAR WITH PAUL ALLISON
Here is Paula’s project, co-authored with Eman Abdelhadi. They have a large, cross-sectional sample of adult women from approximately 50 countries. They are estimating a logistic regression model for a dichotomous dependent variable: whether or not a woman is employed. One of the independent variables is also dichotomous: whether or not a woman is a Muslim (coded 1 or 0). In order to control for all between-country differences, they estimate a between-within model with the following characteristics:
- a random-intercepts model with countries as clusters.
- a “within” predictor that is the Muslim indicator (dummy variable) minus the country mean of that variable.
- a “between” predictor that is the country mean, i.e., the proportion Muslim.
- other control variables at both the person level and the country level.
The coefficient for the within predictor is very close to what you would get from a classic fixed effects estimator, as estimated by conditional logistic regression. (My 2014 post discusses why they are not identical). So it represents the effect of being Muslim on employment, controlling for all country-level variables, both observed and unobserved.
Here is the question. Can you interpret the coefficient for the between predictor (proportion Muslim) as the effect of living in a country that is more or less Muslim, regardless of whether a person is personally a Muslim? In other words, can you interpret the between coefficient as a contextual effect?
Surprisingly, the answer is no. By construction, the within variable is uncorrelated with the between variable. For that reason, the coefficient for proportion Muslim does not actually control for the person-level effect of being Muslim.
The reason I never thought about this question before is that I primarily use the between-within model for longitudinal data, with repeated measurements clustered within persons. In that setting, the coefficients for the between variables are usually uninteresting or misleading. But when applied to other kinds of clustering, the estimation and interpretation of “between” effects can be quite important.
Fortunately, there’s a simple solution to the problem: Estimate the model using the original Muslim indicator rather than the deviation from its country-level mean. This model is mathematically equivalent to the original between-within model—the coefficients for the Muslim indicator and for all the control variables will be exactly the same. But the coefficient for the proportion Muslim will change, and in a predictable way. Here is the algebra:
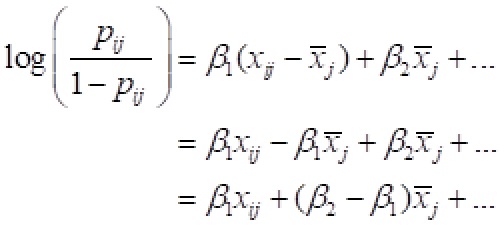
In these equations pij is the probability of employment for person i in country j, xij is the Muslim indicator for person i in country j, and x-bar-j is the mean of the Muslim indicator in country j.
The first equation is the usual formulation of the between-within model. The second equation is the algebra that gets us to the third equation. That equation is the new formulation of the model with xij and x-bar-j as predictors. Notice that the coefficient of x-bar-j in the third equation can be found by subtracting the coefficient for the within effect from the coefficient for the between effect in the first equation.
So you don’t actually have to re-estimate the model to get the contextual effect. You can just take the difference in the coefficients in the standard between-within model. Furthermore, testing whether those coefficients are the same or different (which is usually done to test fixed vs. random effects) is equivalent to testing for the existence of a contextual effect.
Keep in mind that although the coefficient for x-bar-j in the third equation can be interpreted as a contextual effect, it does not control for any unobservables. So it could be biased by the omission of country-level variables or person-level variables that affect employment and are correlated with proportion Muslim. Note, also, that the fact that the person-level variable is dichotomous in this example is completely incidental. The same logic would apply if xij were continuous.
Comments
Thank you for this clarification. In the example above, the nesting includes individuals within counties. I was wondering if the same strategy should be employed if you want to properly interpret the between-individual coefficient when using longitudinal data (i.e., repeated measurements clustered in persons)?
The answer is yes, however, in the longitudinal setting, contextual effects are generally less meaningful. To use the example in the post, if a person is living in a country with a high proportion of Muslims, he or she is potentially affected by all the individuals in that country and the general culture that those individuals produce and enact. For longitudinal data, on the other hand, it is less sensible to think that the person at time t is affected by the average of all the values of the predictors at all points in time.