Marginal Structural Models - Online Course
A 3-Day Livestream Seminar Taught by
Daniel Westreich10:00am-12:30pm (convert to your local time) Thursday-Saturday
1:30pm-4:00pm Thursday, 1:30pm-3:30pm Friday & Saturday
This seminar is an introduction to marginal structural models (MSMs) from both a theoretical and applied standpoint. Marginal structural models (typically fit with inverse probability weights) are increasingly used for causal inference in observational data.
Such approaches are essential to the analysis of longitudinal data with time-varying treatments and confounders. They can yield correct estimates even when traditional methods (such as a time-dependent Cox proportional hazards model) would produce a biased result. The class format will be a mix of didactic lecture, interactive “journal club”, and in-class programming exercises.
Starting October 27, we are offering this seminar as a 3-day synchronous*, livestream workshop held via the free video-conferencing software Zoom. Each day will consist of two lecture sessions which include hands-on exercises, separated by a 1-hour break. You are encouraged to join the lecture live, but will have the opportunity to view the recorded session later in the day if you are unable to attend at the scheduled time.
*We understand that finding time to participate in livestream courses can be difficult. If you prefer, you may take all or part of the course asynchronously. The video recordings will be made available within 24 hours of each session and will be accessible for four weeks after the seminar, meaning that you will get all of the class content and discussions even if you cannot participate synchronously.
Closed captioning is available for all live and recorded sessions.
More details about the course content
Marginal structural models are most usefully applied to longitudinal data when three conditions hold:
- treatments vary with time
- potential confounders vary with time
- confounders may also act as mediators.
In this situation, standard methods almost always yield biased results.
Consider a simple causal scenario, illustrated by a directed acyclic graph (DAG):
 The goal is to estimate the total effect of Treatment at times 0 and 1 on the Outcome. The variable Z is a mediator of the causal effect of Treatment0 on the Outcome (Treatment0 → Z → Outcome), but also a confounder of the causal effect of Treatment1 on the Outcome (Treatment1 ← Z → Outcome).
The goal is to estimate the total effect of Treatment at times 0 and 1 on the Outcome. The variable Z is a mediator of the causal effect of Treatment0 on the Outcome (Treatment0 → Z → Outcome), but also a confounder of the causal effect of Treatment1 on the Outcome (Treatment1 ← Z → Outcome).
Because Z is a confounder, we must control for Z. If we do that using typical regression approaches, we will hold Z constant at each possible level of Z. In a DAG, this is illustrated by placing a box around Z, and that has the effect of removing all arrows out of Z (if Z is held constant, it cannot affect other variables). Here’s the new DAG:
 Unfortunately, this control for Z has removed the effect of Treatment0 on the Outcome, because (again) Z was a mediator of that causal effect. Thus, regression control for Z does not allow us to assess the total effect of both Treatment0 and Treatment1 on the Outcome. But lack of regression control for Z would lead to a biased assessment of the effect of Treatment1 on the Outcome.
Unfortunately, this control for Z has removed the effect of Treatment0 on the Outcome, because (again) Z was a mediator of that causal effect. Thus, regression control for Z does not allow us to assess the total effect of both Treatment0 and Treatment1 on the Outcome. But lack of regression control for Z would lead to a biased assessment of the effect of Treatment1 on the Outcome.
This “damned if you do, damned if you don’t” scenario is resolved if we can analytically remove the arrow from Z to Treatment1, as in the third DAG, below. In this DAG, we can assess both the effect of Treatment1 on the Outcome (which is now unconfounded by Z) while still assessing the effect of Treatment0 on the Outcome (since the pathway Treatment0 → Z → Outcome remains present).
 Now the question is, how can we remove the Z → Treatment1 arrow? While there are multiple ways to approach this problem, marginal structural models based on inverse probability weights (which are closely related to propensity scores) are perhaps the most natural and intuitive, as well as the most widely known.
Now the question is, how can we remove the Z → Treatment1 arrow? While there are multiple ways to approach this problem, marginal structural models based on inverse probability weights (which are closely related to propensity scores) are perhaps the most natural and intuitive, as well as the most widely known.
This seminar will start by reviewing the fundamental ideas of causal inference in observational studies, including potential outcomes, counterfactual thinking, causal identification conditions, DAGs, and alternative approaches to causal thinking. We will then introduce time-fixed marginal structural models, including introductions to inverse probability weights and the g-formula. We will review and discuss relevant literature and work through examples of these ideas in code.
After this we will introduce time-varying MSM with inverse probability weights, including discrete time hazard models and data structures essential to understanding those models. We’ll also work through both literature and code examples of these time-varying MSMs. Finally, we will discuss several advanced topics, including some basics of the time-varying parametric g-formula.
Overall, this seminar will prepare you to both recognize situations in which MSM should be applied and provide you with worked examples of code to enable you to apply these methods in your own work. See the computing section below for more details.
Before coming to the seminar, you should read:
Petersen et al. (2006) Assessing the effectiveness of antiretroviral adherence interventions: Using marginal structural models to replicate the findings of randomized controlled trials.
Robins et al. (2000) Marginal structural models and causal inference in epidemiology.
Marginal structural models are most usefully applied to longitudinal data when three conditions hold:
- treatments vary with time
- potential confounders vary with time
- confounders may also act as mediators.
In this situation, standard methods almost always yield biased results.
Consider a simple causal scenario, illustrated by a directed acyclic graph (DAG):
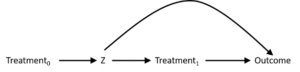
Because Z is a confounder, we must control for Z. If we do that using typical regression approaches, we will hold Z constant at each possible level of Z. In a DAG, this is illustrated by placing a box around Z, and that has the effect of removing all arrows out of Z (if Z is held constant, it cannot affect other variables). Here’s the new DAG:
Unfortunately, this control for Z has removed the effect of Treatment0 on the Outcome, because (again) Z was a mediator of that causal effect. Thus, regression control for Z does not allow us to assess the total effect of both Treatment0 and Treatment1 on the Outcome. But lack of regression control for Z would lead to a biased assessment of the effect of Treatment1 on the Outcome.
This “damned if you do, damned if you don’t” scenario is resolved if we can analytically remove the arrow from Z to Treatment1, as in the third DAG, below. In this DAG, we can assess both the effect of Treatment1 on the Outcome (which is now unconfounded by Z) while still assessing the effect of Treatment0 on the Outcome (since the pathway Treatment0 → Z → Outcome remains present).
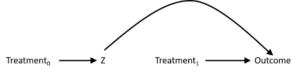
This seminar will start by reviewing the fundamental ideas of causal inference in observational studies, including potential outcomes, counterfactual thinking, causal identification conditions, DAGs, and alternative approaches to causal thinking. We will then introduce time-fixed marginal structural models, including introductions to inverse probability weights and the g-formula. We will review and discuss relevant literature and work through examples of these ideas in code.
After this we will introduce time-varying MSM with inverse probability weights, including discrete time hazard models and data structures essential to understanding those models. We’ll also work through both literature and code examples of these time-varying MSMs. Finally, we will discuss several advanced topics, including some basics of the time-varying parametric g-formula.
Overall, this seminar will prepare you to both recognize situations in which MSM should be applied and provide you with worked examples of code to enable you to apply these methods in your own work. See the computing section below for more details.
Before coming to the seminar, you should read:
Petersen et al. (2006) Assessing the effectiveness of antiretroviral adherence interventions: Using marginal structural models to replicate the findings of randomized controlled trials.
Robins et al. (2000) Marginal structural models and causal inference in epidemiology.
Computing
The exercises for this seminar will primarily (but not exclusively) use SAS. However, equivalent R code with commentary will also be available. To participate in the exercises, you should have access to a computer with SAS 9.4 or a recent version of R installed.
You should have solid familiarity with the use of SAS or R, including opening and executing data files and programs, and a basic understanding of running regression models.
There is now a free version of SAS, called SAS OnDemand for Academics, that is available to anyone.
If you’d like to take this course but are concerned that you don’t know enough R, there are excellent on-line resources for learning the basics. Here are our recommendations.
The exercises for this seminar will primarily (but not exclusively) use SAS. However, equivalent R code with commentary will also be available. To participate in the exercises, you should have access to a computer with SAS 9.4 or a recent version of R installed.
You should have solid familiarity with the use of SAS or R, including opening and executing data files and programs, and a basic understanding of running regression models.
There is now a free version of SAS, called SAS OnDemand for Academics, that is available to anyone.
If you’d like to take this course but are concerned that you don’t know enough R, there are excellent on-line resources for learning the basics. Here are our recommendations.
Who should register?
You should be familiar with regression modeling (including both coursework and application). Some familiarity with ideas in causal inference such as causal diagrams and potential outcomes would be helpful but is not required. If you wish to gain that familiarity, you could read Chapter 3 of the instructor’s textbook Epidemiology By Design or Part I of Causal Inference: What If? by Hernán and Robins (available free on the web). The class is appropriate for epidemiologists, biostatisticians, data scientists, and social scientists generally. However, it will primarily be taught through the lens and vocabulary of epidemiology.
You should be familiar with regression modeling (including both coursework and application). Some familiarity with ideas in causal inference such as causal diagrams and potential outcomes would be helpful but is not required. If you wish to gain that familiarity, you could read Chapter 3 of the instructor’s textbook Epidemiology By Design or Part I of Causal Inference: What If? by Hernán and Robins (available free on the web). The class is appropriate for epidemiologists, biostatisticians, data scientists, and social scientists generally. However, it will primarily be taught through the lens and vocabulary of epidemiology.
Seminar outline
Day 1: Causal inference and introduction to time-fixed MSM.
1. Causal inference in epidemiology
-
-
- Counterfactuals/potential outcomes
- Well-defined interventions
- Causal identification conditions
- DAGs & confounding
2. Introduction to time-fixed marginal structural models
-
-
- Randomization
- Inverse probability weights
- The g-formula
3. Implementation of time-fixed MSM with the g-formula
Day 2: Time-fixed MSM and introduction to time-varying MSM
4. Time-fixed MSM theory
5. Implementation of time-fixed MSM with inverse probability weights
6. Introduction to time-varying MSM
-
-
- DAG examples
- Data structures
- Discrete time hazard models
- More on inverse probability weights
Day 3: Time-varying MSM and additional topics
7. Time-varying MSM theory
8. Implementation of time-varying MSM with inverse probability weights
9. Selected topics
-
-
- Timescale
- Time-varying parametric g-formula
Day 1: Causal inference and introduction to time-fixed MSM.
1. Causal inference in epidemiology
-
-
- Counterfactuals/potential outcomes
- Well-defined interventions
- Causal identification conditions
- DAGs & confounding
-
2. Introduction to time-fixed marginal structural models
-
-
- Randomization
- Inverse probability weights
- The g-formula
-
3. Implementation of time-fixed MSM with the g-formula
Day 2: Time-fixed MSM and introduction to time-varying MSM
4. Time-fixed MSM theory
5. Implementation of time-fixed MSM with inverse probability weights
6. Introduction to time-varying MSM
-
-
- DAG examples
- Data structures
- Discrete time hazard models
- More on inverse probability weights
-
Day 3: Time-varying MSM and additional topics
7. Time-varying MSM theory
8. Implementation of time-varying MSM with inverse probability weights
9. Selected topics
-
-
- Timescale
- Time-varying parametric g-formula
-
Payment information
The fee of $995 includes all course materials.
PayPal and all major credit cards are accepted.
Our Tax ID number is 26-4576270.
The fee of $995 includes all course materials.
PayPal and all major credit cards are accepted.
Our Tax ID number is 26-4576270.

